Mathematical models for biological invasions - competition for open spaces
Fugo TAKASU, Madoka Shiraishi, Kohkichi KAWASAKI*, Nanako SHIGESADA
Department of Information and Computer Sciences, Nara Women's University, Nara 630-8506, Japan
*Department of Knowledge Engineering and Computer Sciences, Doshisha University, Tanabe-cho, Kyoto 610-0321, Japan
Biological Invasions of Ecosystem by Pests and Beneficial Organisms, ed. by E. Yano, K. Matsuo, M, Shiyomi & D. A. Andow, 1999, pp. 78-87.
Proceedings of an International Workshop on Biological Invasions of Ecosystem by Pests and Beneficial Organisms, Tsukuba, Japan, February 25-27, 1997.
Published by the National Institute of Agro-Environmental Sciences, Tsukuba, Japan, NIAES Series 3
ISBN4-931508-00-6
Abstract : A mathematical model for invasions of two competing species into open spaces is presented. One species is assumed to be fugitive, that is, competitively weaker than but superior in diffusive capability to the other species. To describe dispersal and competition, diffusion-reaction equations are used. We consider two types of open spaces: one is an infinite expanse of open space and the other is a finite open space created by disturbances, the size and the interval of which are given as some stochastic variables. Analyzing the model under such environmental conditions, we examine how the fugitive species could escape from the stronger competitor to expand its range, and how often disturbances should occur to maintain coexistence between the two competing species.
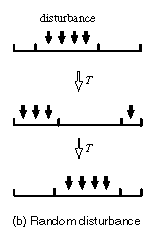
空間構造を含む2種競争系において撹乱が2種共存に及ぼす効果を数理モデルを用いて解析した。ここでいう撹乱とは2種とも根こそぎ取り除くことを意味する。具体的には、山火事、洪水、土砂崩れなどが相当し、新たに生じた「空き地」を巡って生物が侵入と競争を行う状況をモデル化した。競争には優位だが移動分散能力に劣る種と、競争には劣位なものの移動分散に勝る種(放浪種:Fugitive species)との共存は、どのような条件下(どのような撹乱)で可能になるのだろうか?2種共存の条件を、撹乱の頻度、場所、確率性などに注目して解析した。上図は撹乱が無作為の場所に起こる例。
takasu@ics.nara-wu.ac.jp

